Greatest Common Divisor Program Python
The full form of GCD is ' Greatest Common Divisor'. Which means the greatest common factor of the two numbers.
It is also known by the name HCF(Highest common factor). I will be using both the words so don't confuse yourself.I have used for loop, if-else statement, min function and break statement.We have checked both numbers by dividing them every number less than the minimum of both the numbers. And if that number divides both the numbers without leaving any remainder than that number becomes the HCF of the given numbers. And remember that I am running the loop in reverse order. Code: # taking first numbernum1 = int(input('Enter first number: '))# taking second numbernum2 = int(input('Enter second number: '))gcd = 1# finding GCDfor i in range(min(num1,num2),0,-1):if (num1%i) 0 and (num2%i) 0:gcd = ibreak# printing GCDprint('The GCD of the two numbers is ', gcd) Output.
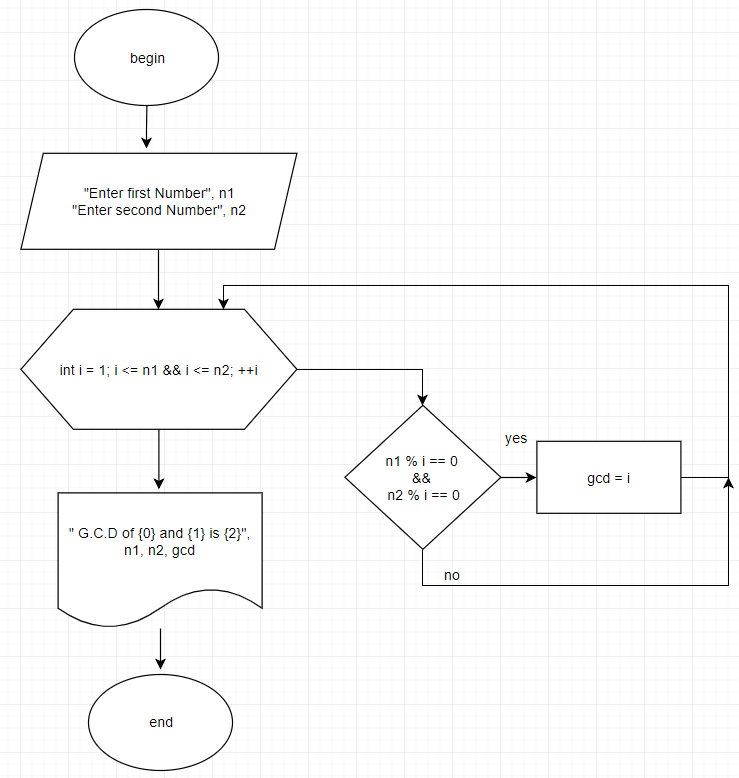
Enter first number: 28Enter second number: 63The GCD of the two numbers is 7We can use Euclid's Algorithm to solve this problem much faster.Finding GCD or HCF of two numbers using Euclid's algorithm in pythonIn this method, we are going to use Euclid's algorithm which is much faster. I have used while loop, if-else statement, and swapping technique. Code: # taking first numbernum1 = int(input('Enter first number: '))# taking second numbernum2 = int(input('Enter second number: '))# checking if num2 is greater than num1 then swap these numbersif num2 num1:(num1,num2) = (num2,num1)# repeat these steps till num2 divides num1 with remainder zerowhile num1%num2!= 0:# swap num1 to num2 and num2 with remainder(num1,num2) = (num2,num1%num2)# printing GCDprint('The GCD of the numbers is ',num2) Output. Enter first number: 28Enter second number: 63The GCD of the numbers is 7We can use Euclid's algorithm with recursion.Finding GCD or HCF of two numbers by Euclid's algorithm using recursion in pythonHere we have made a recursive function gcd. Code: # defining gcd functiondef gcd(num1,num2):if num1%num2 0:# Base casereturn num2else:# Iterative casereturn gcd(num2,num1%num2)# taking first numbernum1 = int(input('Enter first number: '))# taking second numbernum2 = int(input('Enter second number: '))# checking if num2 is greater than num1 then swap these numbersif num2 num1:(num1,num2) = (num2,num1)# printing GCDprint('The GCD of the numbers is',gcd(num1,num2)) Output.
The Greatest Common Divisor ( GCD ) of two integers is the largest integer that divides both of these integers. However, it is not restricted to only two integers, there might be many integers. For the sake of simplicity, we try to build small programmes in Python that facilitate our task of finding GCD of only two integers in this post.There are many methods of finding the greatest common divisor of two numbers a and b, or simply gcd( a, b). Note that gcd(0, 0) is undefined.
Hence, we need to bear in mind this case while writing our program for computing GCD. Trial-Division ApproachLet’s find the greatest common divisor of 24 and 36. The positive common divisors of these numbers are 1, 2, 3, 4, 6, and 12. Therefore, gcd(24, 36) = 12. Here we have found all possible common divisors of 24 and 36, then picked the largest one among them, 12. The first algorithm that we use for our program will be based on this idea.The first important step is to check whether both a and b are equal to 0.
If so, the program will print the warning message and redirect it to the standard error stream.In the heart of the program, we go from 1 to a and check which number divides both a and b. As the loop condition is controlled by variable a, it is vital to make sure that a 0. If a is 0, we return b.
Nolf 2 patch 1.2. No One Lives Forever 2: A Spy in H.A.R.M's Way. Can Cate Archer stay out of H.A.R.M.' S way long enough to avert a nuclear holocaust? 3 update for No One Lives Forever 2 adds a list of new features including Team DM and Doomsday MP modes, gameplay tweaks, and a host of other updates. No One Lives Forever 2: A Spy in H.A.R.M's Way. Can Cate Archer stay out of H.A.R.M.' S way long enough to avert a nuclear holocaust?


Greatest Common Divisor Program In Python
However, what happens if the function gcd(a,b) gets negative arguments? There will be no problem, because gcd(a,b) = gcd(−a,b) = gcd(a,−b) = gcd(−a,−b). Return dAs you can see computing the greatest common divisor of two integers using this algorithm is inefficient.
This makes our python program very slow. We have to look for a more efficient method of finding the greatest common divisor. Euclid’s AlgorithmThis algorithm has been known since ancient times. The ancient Greek mathematician Euclid left us a description of this algorithm in his great book The Elements.Let a = bq + r, where a, b, q, and r are integers. Then gcd(a, b) = gcd(b, r).Proof:Suppose that d divides both a and b. Then it follows that d also divides a − bq = r.
Greatest Common Divisor Program Python 2
Hence, any common divisor of a and b is also a common divisor of b and r.Likewise, suppose that d divides both b and r. Then d also divides bq + r = a. Hence, anycommon divisor of b and r is also a common divisor of a and b.Consequently, gcd(a, b) = gcd(b, r).Going back to our program, we make some changes to its core part, using.